Lab 2

DUE: Nov 14 in class

Bring the solutions in written form to class or upload on Moodle!

Problems are from Gonzalez 4th Ed.

10.14 (10 points)

The results obtained by a single pass through an image of some 2-D kernels can be achieved also by two passes using 1-D kernels. For example, the same result of using a 3x3 smoothing kernel with coefficients 1/9 can be obtained by a pass of the kernel [1 1 1] through an image, followed by a pass of the result with the kernel [1 1 1]^T. The final result is then scaled by 1/9. Show that the response of Sobel kernels (Fig. 10.14) can be implemented similarly by one pass of the differencing kernel [-1 0 1] (or its vertical counterpart) followed by the smoothing kernel [1 2 1] (or its vertical counterpart).

10.30 (15 points)

An important application of image segmentation is in processing images resulting from so-called bubble chamber events. These images arise from experiments in high-energy physics in which a beam of particle of known properties is directed onto a target of known nuclei. A typical event consist of incoming tracks, any one of which, upon a collision, branches out into secondary tracks of particles emanating from the point of collision. Propose a segmentation approach for detecting all tracks angled at any of the following six directions off the horizontal: ±25°, ±50°, and ±75°. The estimation error allowed in any of these six direction is ±5°. For a track to be valid it must be at least 100 pixels long and have no more than three gaps, each not exceeding 10 pixels. You may assume that the images have been preprocessed so that they are binary and that all tracks are 1 thick, except at the point of collision from which they emanate. Your procedure should be able to differentiate between tracks that have the same direction but different origins. (Hint: Base your solution on the Hough transform.)

10.46 (10 points)

Let the pixels in the first row of a 3x3 image, like the one in Fig. 10.55(a) be labeled as 1, 2, 3, and the pixels in the second and third rows be labeled as 4, 5, 6 and 7, 8, 9, respectively. Let the intensity of these pixels be [90, 80, 30; 70, 5, 20; 80 20 30] where, for example, the intensity of pixel 2 is 80 and of pixel 4 it is 70. Compute the weights for the edges for the graph in Fig. 10.55(c), using the formula 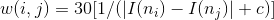explained in the text in connection with that figure (we called the formula by 30 to make the numerical result easier to interpret). Let c = 0 in this case.

11.9 (5 points)

With reference to Fig. 11.6(d), would you expect the snake to converge to the contour if the number of iterations were increased? Explain the rationale for your answer.

11.11 (10 points)

Give a general (parameterized) equation capable of generating an elliptical snake at any location in the image plane, and containing K equally spaced points. Your solution must be discrete and must indicate a specific range for the variables. Your snake must be closed.

11.32 (10 points)

If we let a= -1 and b = 1 in Eq. (11-94), and start with the configuration in the figure below, what would the segmentation contour look like at convergence? (11-94): F(x,y) = af(x,y) + b[1 - f(x,y)]

Total: 60 Points