Lab 3

Light Field Camera

Due: Thu, December 14 2017, 23:59

Start Early!!!

This lab was modeled after the assignment 3 of Stanford's Image Synthesis class.

Light field cameras allow user to capture a 4-dimensional radiance (Light Field) and then use it to synthesize new images with different camera settings by sampling and reconstructing form the light field.

PBRT comes with four built-in cameras: Simple Orthographic and Perspective thin lens models, Environment camera for full 360 degree view, and Realistic camera with data-driven lens system. You will be extending pbrt to include a light field camera, and then extending imgtool to synthesize images using the produced light field.

Step 1: Background Reading

Light fields has been introduced to the graphics literature in 1996 by Levoy and Hanrahan in a SIGGRAPH paper Light Field Rendering. It involves prefiltering the light field before sampling to avoid aliasing, at the expense of only being able to re-render a shallow depth-of-field.

This lab exercise is based on a follow up paper form 2000, Dynamically Reparameterized Light Field with the focus of being able to moderately sample scenes with a wide depth range into a light field, and reconstruct images with widely varying aperture setting and focal planes, even allowing non-planar focal planes.

Step 2: Extend PBRT with Light Field Camera

You will be extending PBRT to have a new camera subclass. The new camera should simulate a 2D array of equally spaced pinhole cameras, called data cameras, with identical resolution and field of view. This configuration is a restricted subset of the configuration in the Dynamically Reparameterized Light Field paper. The lab3_scenes set provides a set of useful scenes for testing your code and submit your results.

To add a new camera, you need to follow the same procedure as lab-2. Create two new files lightfield.h and lightfield.cpp, which include the code for the new camera subclass. Provide a CreateLightFieldCamera(...) to prepare the camera and call it form api.cpp, where the camera parameters are parsed and camera instances are created. You should parse "shutteropen", "shutterclose" and "fov" in the same way perspective camera does. Further, you should accept the parameters "camerasperdim" and "cameragridbounds". For example, the following line should create a light field camera with 256 data cameras (each with a 50 degree field of view) arranged in a 16x16 grid, on the light field camera's z=0 plane, equally spaced within the xy bounding box that goes from [-0.6] to [0.6] in both dimensions (the parameters to "cameragridbounds" are [minX, maxX, minY, maxY] ) 

Camera "lightfield" "float fov" [ 50 ] "integer camerasperdim" [16 16] 
       "float cameragridbounds [-0.6 0.6 -0.6 0.6]"

The images of all data cameras are generated in a 2D array of sub-images in a large image. The following image is an example output of a lightfield camera, rescaled to 1024x1024 resolution. The image is split to 16x16 camera array, where each square corresponds to a single data camera. The top-left sub-image corresponds to the top-left data camera in the camera array. Similarly, the top-left corner of the sub-image corresponds to the to-left corner of the data-camera's view.

To implement this you will need to write your own LightfieldCamera::GenerateRay() function (overriding the base class's). Note that to get correct ray differentials at the boundary between different data cameras you will also need to override Camera::GenerateRayDifferential(). You do not need to implement any other function defined in Camera.

Both of these functions take in a CameraSample and return a Ray and a floating point weight for the ray to be used in the Monte Carlo estimation. In a pinhole camera model, all rays are created equal (contribute equal weight to the Monte Carlo estimation) so we can just return 1.0. The interesting part is generating the ray in the first place. The CameraSample has three member variables: pFilm, which provides the location of the sample on the film plane (if the film is [width x height] pixels, the values will be on the range [0,width)x[0,height), with 0.5 corresponding to pixel centers). pLens provides the location of the sample on the lens in a parameterized uv space on the unit square; for a camera with a lens we'd have to do an equal area transform so that this became a sample on the lens disk, but for pinhole cameras the "lens" is a single point so this can be ignored. time provides the time the ray is cast; this is useful if you have an animated scene; we do not, but pass this value along to your ray anyways.

The origin of your ray will be at the camera's origin (the pinhole). You only need to calculate the direction of the ray based on where it is on the film plane and your camera's field of view. The pinhole camera section of PBRT 1.2.1, and the section on perspective cameras should help significantly with your understanding; but as a recap, rays on the middle of the film plane should come straight out of the camera; rays on the far edge of the film plane should make a tan(fov/2) angle with the middle ray; the angle on the x axis does not depend on the y coordinate and vice versa. It easiest to construct your ray in camera space, and transform it using CameraToWorld afterwards.

For LightfieldCamera::GenerateRayDifferential() you will want to implement it so that each data camera has the same ray differentials it would have had at the boundary if it was a regular pinhole camera that was not sharing a film plane. The default implementation will have massive incorrect jumps at data camera boundaries; see PBRT 6.1.

You will want to render the original settings for book.pbrt as soon as possible to have a well-sampled light field to work with (it may take several hours to generate, so you'll want to run it over night if possible), but for now turn down the resolution so there are only 8x8 data cameras with 128^2 resolution each, which should be 64x faster to generate.

Step 3: Synthesize a Final Image from the LightField

In this step we will add an extra feature to imgtool command to synthesize an image using the pre-rendered light field. You will need to modify the imgtool source code at tools/imgtool.cpp to add the functionality.

We start with adding the new command to the usage string:

lightfield options:
    --camsperdim <x> <y>                    Number of data cameras in the X and 
                                            Y direction, respectively
    --camerapos <x> <y> <z>                 Position of the desired camera for 
                                            reconstruction (treating the data
                                            camera plane as z = 0)
    --filterwidth <fw>                      Width of the reconstruction filter (in
                                            meters on the camera plane)
    --focalplanez <fz>                      Z position of the focal plane for 
                                            reconstruction (treating the data
                                            camera plane as z = 0)
    --griddim <xmin> <xmax> <ymin> <ymax>   The bounding box of the data cameras
                                            positions in the x and y dimensions 
                                            (in meters)
    --inputfov <f>                          FOV (in degrees) of the input 
                                            lightfield data cameras
    --outputfov <f>                         FOV (in degrees) of the output image
    --outputdim <w> <h>                     Output size in pixels per dimension

Modify the main() function to call the lightfield() function (which you will be implementing) when the first command line argument is "lightfield". Here is a skeleton of the lightfield function that parses the arguments specified in the usage string (without much error handling!), reads the light field image (sometimes referred to as the ray database), and saves an output image (without writing useful values to it):

int lightfield(int argc, char *argv[]) {
  
    const char *outfile = "resolvedLightfield.exr";
    Bounds2f griddim(Point2f(0, 0));
    float inputfov = 90.0f;
    float outputfov = 45.0f;
    Vector2i camerasPerDim(1, 1);
    Point2i outputDim(256, 256);
    float filterWidth = 0.05f;
    float focalPlaneZ = 10.0f;
    Point3f cameraPos(0,0,-0.02f);
    int i;
    for (i = 0; i < argc; ++i) {
        if (argv[i][0] != '-') break;
        if (!strcmp(argv[i], "--inputfov")) {
            ++i;
            inputfov = atof(argv[i]);
        } else if (!strcmp(argv[i], "--outputfov")) {
            ++i;
            outputfov = atof(argv[i]);
        } else if (!strcmp(argv[i], "--camsperdim")) {
            ++i;
            camerasPerDim.x = atoi(argv[i]);
            ++i;
            camerasPerDim.y = atoi(argv[i]);
        } else if (!strcmp(argv[i], "--outputdim")) {
            ++i;
            outputDim.x = atoi(argv[i]);
            ++i;
            outputDim.y = atoi(argv[i]);
        } else if (!strcmp(argv[i], "--camerapos")) {
            ++i;
            cameraPos.x = atof(argv[i]);
            ++i;
            cameraPos.y = atof(argv[i]);
            ++i;
            cameraPos.z = atof(argv[i]);
        } else if (!strcmp(argv[i], "--griddim")) {
            ++i;
            griddim.pMin.x = atof(argv[i]);
            ++i;
            griddim.pMax.x = atof(argv[i]);
            ++i;
            griddim.pMin.y = atof(argv[i]);
            ++i;
            griddim.pMax.y = atof(argv[i]);
        } else if (!strcmp(argv[i], "--filterwidth")) {
            ++i;
            filterWidth = atof(argv[i]);
        }  else if (!strcmp(argv[i], "--focalplanez")) {
            ++i;
            focalPlaneZ = atof(argv[i]);
        } else {
            usage();
        }
    }
    if (i + 1 >= argc)
        usage("missing second filename for \"lightfield\"");
    else if (i >= argc)
        usage("missing filenames for \"lightfield\"");

    const char *inFilename = argv[i], *outFilename = argv[i + 1];
    Point2i res;
    std::unique_ptr image(ReadImage(inFilename, &res;));
    if (!image) {
        fprintf(stderr, "%s: unable to read image\n", inFilename);
        return 1;
    }

    std::unique_ptr outputImage(new RGBSpectrum[outputDim.x*outputDim.y]);

    // Render from your lightfield here...

    WriteImage(outFilename, (Float *)outputImage.get(), Bounds2i(Point2i(0, 0), outputDim),
        outputDim);
    return 0;
}

When you run imgtool, "camsperdim", "griddim", and "inputfov" should match the values used to generate the light field image in the first place. "outputdim" defines the size of the output image, "camerapos" positions the synthetic camera, "outputfov" sets up the field of view of the output camera, and "focalplanez" defines the focal plane for the synthetic camera. We will be using the phenomenological model laid out in Dynamically Reparameterized Light Fields for reconstruction in this section: "filterwidth" implicitly controls the effective aperture size of the synthetic camera in this model; but we will be revisiting this approach in a later section of the assignment. The desired camera is assumed to have the same rotation as the data cameras, pointing down their Z axis with the same up vector they have.

Note that the input light field and output image are stored in a flat array of RGBSpectrum. These images are stored in row-major order (all the pixels of the first row are first, then all pixels of the second row, etc). RGBSpectrum wraps up RGB values used to store radiance/irradiance/sensor response; RGBSpectrums has defined multiplication by a Float, so you never need to actually grab the values out to implement things like a weighted average of radiances.

Recall from class that evaluating the response of a camera involves solving a five dimensional integral; 2 dimensions for the sensor's pixel area, 2 dimensions for the directions of incoming light, and 1 dimension for time. For now, we will be assuming that the light field image is capturing a particular moment in time, and the synthetic camera we are rendering to is static; this removes the time dimension from the integral. For this section only, we will ignore the 2 dimensions of pixel area for the synthetic camera sensor, evaluating only the light incident on the pixel's center.

This leaves the two dimensions corresponding to the incoming light direction. Instead of solving this using a Monte Carlo estimator, Dynamically Reparameterized Light Fields approximates this integral by evaluating a weighted average of individual rays in several data cameras. Recall that our ray database is a finite discrete sampling of the 4D light field; since the space of rays is continuous, that means the probability that we have that exact ray in the light field image is 0. If we want to sample a ray (say to get the value for a pixel of the output image using the desired camera), we need to interpolate the ray from "nearby" rays in the ray database.

For this section we will use a three step procedure to reconstruct the ray. First, we will find where the ray intersects the data camera plane (at coordinates s,t) and the focal plane (at coordinates f,g). Then we will find all data cameras within the filter radius of s,t; and take a weighted sum of the radiance values stored in the ray database for all rays leaving said data cameras and intersecting (f,g). This is illustrated in figure 4 of the paper (in our case F-plane and C-plane are parallel since we do not have camera rotations.):

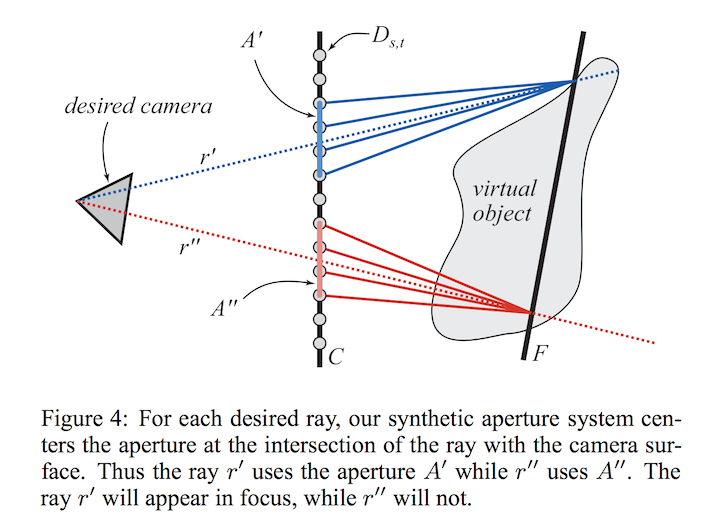
Notice that this is a weighted sum of rays that focus on the same point as the initial ray; they are samples that could have been drawn to evaluate irradiance if we were doing Monte Carlo integration of the irradiance and our lens subtended the same area as our filter. That is precisely the approximation we are making (along with our ad-hoc weights; consider why this is a biased approximation); this is a phenomenological approach; it reproduces the effect of defocus blur but is not physically correct.

There are two unanswered questions in how to implement the above approach:

Once you have correctly implemented this section, you should be able to run:

Change the settings (while keeping the filter width roughly the same) so that the author's names are well focused and generate an image to submit.

Step 4: A Monte Carlo Approach

In step 3 we leverage the work of Isaksen et. al to quickly generate plausible final renderings from the light field. To do so, we gave up accurate modelling of the desired camera to have an easily formulated algorithm for generating final pixel values. In this step, we will instead perform Monte Carlo integration to solve the camera equation:

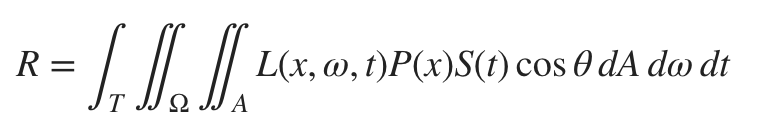
The only primitive operation we need from the light field to solve this equation is a mapping form a ray r(x,w,t) to L(x,w,t). In step 3, we freely combined the solid angle integration with this mapping. In this step we will instead attempt to isolate the mapping and let Monte Carlo integration take care of the rest.

We can reuse most of our infrastructure from Step 3. We can still find rays in the data cameras using the same approach., but we will interpolate the final rays from the data camera rays using bilinear interpolation. This drastically decreases the size of our reconstruction filter and gives us a more plausible estimate of the radiance coming in along a single ray.

Now we can mimic any camera/film setup in pbrt by "tracing" rays the same way in this light field as we would have in the original scene; with the difference that no actual tracing happens in the light field, and we just look up the ray in the ray database using two-stage bilinear interpolation.

Add these parameters to your imgtool lightfield usage instructions: 

--montecarlo                        If this flag is passed, use Monte Carlo
                                    integration generate the final image
                                    (this renders filterwidth useless)
--lensradius <r>                    The radius of the thin lens in the 
                                    thin lens approximation for the output
                                    camera.
--samplesperpixel <p>               The number of samples to take (per pixel)
                                    in Monte Carlo the integration of the 
                                    final image.

They should have the following defaults:

bool monteCarlo = false;
        float lensRadius = 0.0f;
        int samplesPerPixel = 1;

and here is some argument parsing code (to add into the parsing code in Step 3) you can add if you do not want to write it from scratch:

if (!strcmp(argv[i], "--montecarlo")) {
      monteCarlo = true;
  } else if (!strcmp(argv[i], "--lensradius")) {
      ++i;
      lensRadius = atof(argv[i]);
  }  else if (!strcmp(argv[i], "--samplesperpixel")) {
      ++i;
      samplesPerPixel = atoi(argv[i]);
  }

Note that the focal plane is specified relative to the data camera plane, not the desired camera. Once you have the parameters all set, you can perform Monte Carlo integration of the integral:

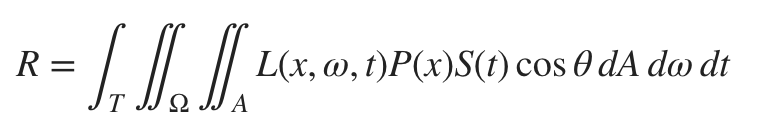
For this assignment, we assume a static scene and camera, so the time integral goes away:

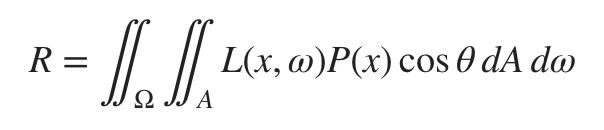
We can solve this integral using a Monte Carlo estimator that samples rays whose origins are sampled from the sensor area and whose directions are sampled from all directions that hit the lens. We will be using the thin lens approximation (detailed in pbrt 6.2.3 and in lecture, and implemented in perspective.cpp for pbrt's perspective camera). We will follow pbrt and simplify our Monte Carlo estimator; throwing out the cosine term and weight from the solid angle integration integration (the thin lens model already used a paraxial approximation, which threw this exactness out the window).

Our estimator will reduce to simple average of radiance values for rays sampled in the method defined by pbrt 6.2.3 per pixel. In order to do Monte Carlo integration you will need to be able to generate random numbers (see the RNG class) and transform a sampling of the unit square to a sampling of the unit disk (for the lens); you will be sampling random points on the sensor pixel and random points on the lens for every ray in the estimator. See ConcentricSampleDisk().

Reproduce your final image from Step 3 using your newly implemented Monte Carlo method. It will necessarily be slightly different since we are now using a more accurate approximation. Make sure to keep track of the command lines you use to generate each image.

Download the ecosys scene. There is already a light field rendered (it took ~10 hours to render on a mid-range desktop) in ecosys_lightfield.exr. The light field image is at 8192x8192 resolution with 64 samples per pixel; and the camera settings were:

Camera "lightfield" 
      "float fov" [ 60 ] "integer camerasperdim" [16 16] 
      "float cameragridbounds" [-2.5 2.5 -1.5 1.5]
All other settings were identical to those in ecosys.pbrt. The following picture shows one of the data camera images from ecosys_lightfield.exr.

Render and image using the thin-lens camera specified in ecosys.pbrt. Render an image using the same camera parameters from the ecosys_lightfield.exr instead. You can select the samples per pixel, so long as the two images are roughly comparable. These images both demonstrate an interesting effect: with a wide enough lens, and by focusing on the far hilside, we can effectively "see through" the trees. Explain why this happens and describe the difference between the two images.

Produce two other images by moving the camera and focal plane to focus on the two trees (one tree per image!) visible in the light field (and in the original image). You may narrow the lens radius but make sure it is above zero. Feel free to generate new light fields with higher or lower angular resolution, spatial resolution, spatial separation, or samples per pixel if it improves your results. You will almost certainly have noticeable visual artifacts in your images; that is fine, but provide an explanation for why they exist, how you mitigated them, and how you would alleviate them given more time to generate the light field.

Step 5: Optional Bonuses

There are several interesting extensions you can make to this project. You may choose one of the below, augment your imgtool implementation, and document what you have done. Produce at least two distinct images:

Step 6: Short Discussions

HINTS

  • When implementing the light field camera, break it down into stages. For example, first implement a standard pin-hole camera. Then implement a grid of pin-hole camera with the same origin, then arrange the camera origins in the specified grid.
  • When implementing imgtool's lightfield function, again, break it down into stages; there are a lot of small parts you need to get right to get the final result. For example, have it output the upper-left corner of the lightfield, then position the camera at one of the data cameras and implement the full algorithm, and see if the result is reasonably close to the data camera's result. Then move the camera and/or change the filter width.

    • SUBMISSION

    To submit your work, create a .zip or .tar.gz file that contains: